You may be familiar with the rules for setting A* in the current A levels: students must get enough UMS marks to achieve a grade A overall and achieve 90% or more of the UMS marks at A2. This rule has been in place since the A* was first awarded in 2010.
In the new, linear A levels it’s much more straightforward. There are no UMS marks, and all the papers are A level papers. Exam boards will use predictions to identify an overall subject-level grade boundary for A*, and students who achieve that mark or higher will get an A*.
Here’s an example to show how that will work. (Note that this is an over-simplified example. In many specifications this summer, one or more of the paper marks will be scaled to achieve the correct weighting for that paper.)
Imagine a new linear A level, with two papers
Paper 1 is marked out of 60 marks and is worth 60% of the A level qualification.
Paper 2 is marked out of 40 marks and is worth 40% of the A level qualification.
Students’ marks on paper 1 will be added to their marks on paper 2 to get a ‘subject-level mark’ (also referred to as a qualification-level mark). In this case, that means each student will get a subject-level mark out of 100.
The exam board will add the marks for each paper together for each student, and create a subject-level mark distribution for all students, starting from the maximum mark and showing the cumulative percentage of students at each mark, from 100 down to zero.
At A* (and A and E) exam boards will have a prediction (based on prior attainment) for the expected percentage of students who will achieve the grade. We have already said that exam boards will put greater emphasis on predictions this year, to avoid unfairly disadvantaging this year’s cohort. We know from our research into the sawtooth effect that, in general, students perform less well in the first year of a new qualification.
In our example, let’s say that at A* the prediction is 7.2%. The exam board will look at the mark distribution for the subject and identify the mark where the cumulative percentage is closest to 7.2. in this case that’s a mark of 76. The exam board will therefore set the subject-level grade boundary for A* at 76 marks out of 100.
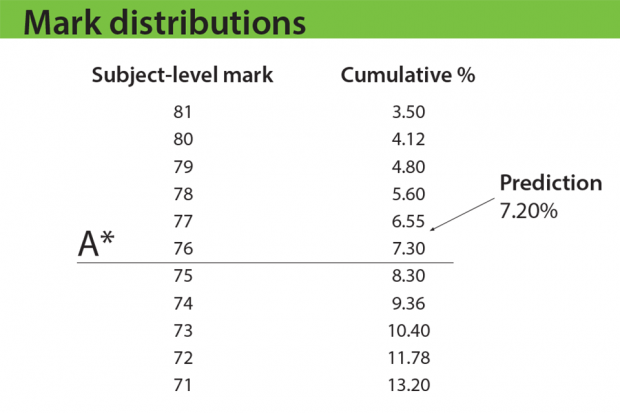
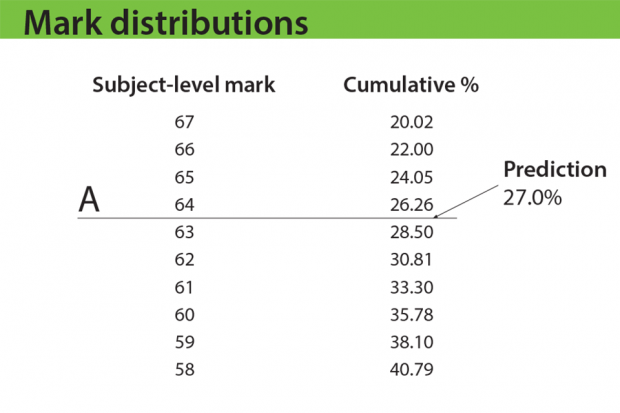
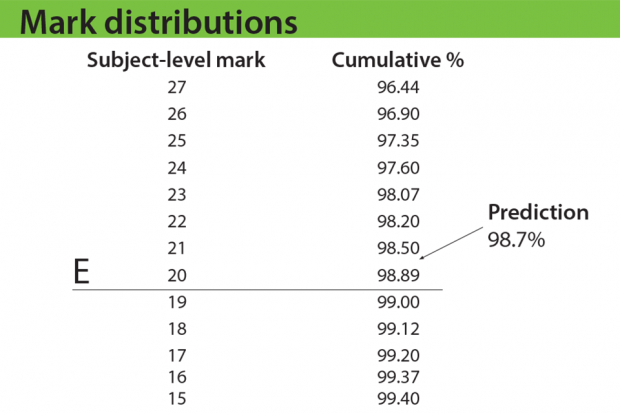
Exam boards will follow a similar approach with A and E – see examples below. But once the mark closest to predictions is identified, senior examiners will be asked to look at some student work, to make sure they are content that the work is appropriate for that grade. They’ll do this for A and E, but not A*, because they have previous experience of reviewing work at grades A and E. Senior examiners have never reviewed work at A* (because it’s always been set using the rule set out above), so they would not be in a position this summer to judge whether work is appropriate at that grade. In future years, we expect senior examiners to review work at A* as well as A and E.
This approach means that as long as a student achieves enough marks at subject level (76 or more in this example), they will receive an A* grade. It doesn’t matter how they get their 76 marks. One student could score full marks (60/60) on paper 1 and 16/40 marks on paper 2 (60+16=76). Another could score 46/60 on paper 1 and 30/40 on paper 2 (46+30=76).
This means that the grade boundaries set at paper level are less important. Exam boards will still publish them, but they are only a guide. The mark that will determine the overall grade is the overall subject-level mark.
A* will continue to identify the very best students, and, broadly speaking, students who would have got an A* in previous years will get an A* in the new A levels.
Cath Jadhav
Associate Director, Standards and Comparability
14 comments
Comment by Jon Thompson posted on
Which prior attainment data will be used to generate the predictions upon which grade boundaries such as A* are based, please? Specifically for A levels in French, German, Spanish and Russian?
Comment by Cath Jadhav posted on
As a general principle, we do not change the prior attainment 'reference year'. Most A levels (reformed and unreformed) therefore continue to use the average of 2010/2011 A level results (and GCSE attainment in 2008/2009). Where we have evidence that the reference year no longer reflects the current situation (for example because entry patterns have changed significantly) we will change the reference year. We have done that in French, German and Spanish because of the changes exam boards have recently made in those subjects. So the predictions will be based on data from A level results in 2016 and students' prior GCSE attainment in 2014.
For Russian, the exam boards will continue to use the 2010/2011 data for predictions. However, the entry numbers in Russian are smaller: as a result there is often no reporting tolerance and exam boards rely more heavily on examiner judgement to set standards.
Comment by Fareed posted on
Will you use the first year or the most recent year of the old spec boundaries for this year's A* boundary I.e. the first year of the new linear spec? E.g. for OCR computer science, the old specification (H047,H447) was introduced in 2009 so the first exam series to complete the a level was Jan 2010 and the most recent year (i.e. the last year of the old spec) exam series was June 2016.
So which exam series grade boundaries will exam boards use for A* in the first series of the new linear exams? Correct me if I'm wrong but I assume it will be the first year of the old spec as the candidates sitting exams in that year would have been subject to the sawtooth effect the same way as the first year of the new spec will be subjected to sitting the first linear exams (in this case the H046,H446 Computer science linear spec).
Assuming this to be true, would it be safe to predict this year's A* grade boundary by using the number of marks needed for an A* in the old H447 spec and dividing it by the total number of marks across all components of that spec (2 AS exams, 1 A2 exam and coursework) then multiplying the percentage by the total number of marks of all the components?
I carried out some calculations for both first and last years of the H447 old spec (Jan 2010 and June 2016) and here's what I found:
For the first year (jan 2010)
A* was 325 marks out of a total of 400 across all 4 components which is 81.25%. Multiplying this percentage by the total number of marks of the new linear spec exams makes an A* 285/350 marks (rounded to the nearest mark). However, this result seemed too high to be plausible since an A in the new spec AS exams was only 61% (86/140).
For the last year (June 2016)
A* was 296 marks out of a total of 400 across all 4 components which is 74% exactly. Multiplying this percentage by the total number of marks in the new linear exams makes an A* 259/350. Although this is not the first year of the old spec, this result seems more reasonable for the boundary of the first year's A*.
I also made one final calculation. The A grade boundary for the new linear spec first AS exam series was 86/140 from both exam components. This was only 61% of the marks need for an A and since an A* is usually no more than 10% of the marks added to the A grade boundary, I multiplied 70% by the A Level total number of marks (350) and calculated the A* boundary to be only 245/350 marks.
I understand grade boundaries will obviously depend on the difficulty of the paper and are calculated after seeing the distribution of marks of all candidates etc. but I would really appreciate if you could shed some light regarding this particular issue. Am I more or less right in saying an A* will be between 245 and 259 marks so around 250/350 marks? Or perhaps I have misunderstood this article.
I'm asking because I am self studying new OCR A level computer science (H046,H446 spec) and got an A overall in last year's AS exam series. Obviously, this being a linear spec, the AS exams don't count but since this year will the first A level exam series that do count and the fact that I am predicted and am aiming for an A* in computer science, I was just wondering what sort of marks would I need to do achieve an A* overall.
Thank you for reading this and I look forward to hearing from you.
Comment by Cath Jadhav posted on
Exam boards will be using prior attainment data (how well the A level computer science cohort did at GCSE) to predict the percentage of students likely to achieve A*, rather than trying to predict the number of marks needed to achieve an A*. For computer science this summer, we are using results in 2016 as the basis of the prediction. This is because the entry has grown in recent years, and so using results from the first year of the old specification might not be a good representation of recent results.
Comment by Andrew posted on
Having been involved with the grading process for the first year of CIE's Pre-U exams back in 2010, a factor that was taken into account was that because it was a linear course with no re-sit opportunities (and no easy AS marks to be gained), the standard required to gain a D3 (A grade equivalent) was lower in Pre-U than that required to gain the UMS marks equivalent to an A in the A2 papers for the OCR new (at that time) A level. You say that Senior Examiners have experience of what standard is required for an A at A level but I trust that the standard that they are familiar with for an A in the old A2 papers will not be used to decide that this should be the level that they think must be achieved across the range of the new linear papers.
Comment by Cath Jadhav posted on
We know that senior examiners will find it more difficult this year to compare linear A level papers with previous A2 units. That's why we have agreed with exam boards that they will prioritise the statistical predictions based on the cohort's prior attainment. Senior examiners will check that the grade boundaries suggested by the statistics are appropriate.
Comment by Ryhana posted on
Hi, I was wondering since I was predicted an A for AQA A level Economics, would this constrain me to only achieving an A in my final grade since the exam board wants the student to achieve a grade based on their prediction? I'd like to know if it is possible for me to still achieve an A* despite an A prediction since I want to outdo my prediction.
Thank you.
Comment by Cath Jadhav posted on
When exam boards use predictions, those predictions are for the whole cohort, not for individual students. Schools and colleges make predictions for individual students but those will not constrain your result. Your actual grade may be higher (or lower) than your predicted grade, depending on how many marks you achieve in the exams.
Comment by Dom posted on
How can we access what these predicted grade boundaries will be?
Comment by Sam Lawrence posted on
Are these example boundaries going to be close to the real thing in subjects like History? 64% for an A seems very low? Or is it because it's a new a level system and the grade boundaries are expected to be quite low?
Comment by Tet posted on
What is preventing exam boards from returning to the old system of having fixed cumulative grade boundaries? e.g. Top 5% get A*, the next 10% get A, and so on. That was so much simpler and clearer. This whole business of moving boundaries (based on "prediction" or UMS or any other method) seems like a tool handed out to the exam boards for the purpose of grade manipulation and inflation for political and business purposes. (Government can pretend that the standard of education is improving and exam boards can try to increase the number of "clients" by giving out higher percentage of good grades, etc.) I can see the advantage of moving boundaries if sample sizes were tiny, but that is clearly not the situation we have.
Comment by Ayesha posted on
When revising for exams can you still do past papers from the old spec as the there is only 1/2 sets of sample papers for the new AS and A-level which isn't enough. (This is for chemistry and biology) 🙂
Comment by hassan posted on
is it all subjects that have this changed where the as grade does not count for the final grade and in what year did you have to start a level for it to apply
Comment by Cath Jadhav posted on
The changes to AS and A level are being phased in over a number of years. If you started your A levels in September 2017, it's likely that most, if not all, will be reformed linear A levels. More detail on the timetable can be found by following this link.